Decision Trees

The STAR Scorecard uses a conditional inference tree algorithm to segment the loan attributes and create the Comp for each metric based on the historical performance of the Fannie Mae book of business. To do this, Fannie Mae uses a publicly available recursive partitioning algorithm4 to choose the loan characteristics that most significantly differentiate performance for each segment of loans.

The recursive partitioning methodology makes a series of binary splits on a large set of control variables, ordering them by how important each variable is to the metric outcome. Once a control variable is selected, the algorithm then decides which split5 best differentiates performance for that variable. As this process is repeated, the series of splits creates a tree-like structure – referred to as a Decision Tree – and each decision point in this tree is referred to as a “node." Once the tree has extended to the point that there are no more variable splits that significantly differentiate performance, the branch terminates into its final, “terminal” node. It is the performance of each servicer’s loans at the terminal node level that is then used to calculate servicers’ Comp for the metric.

Figure 2 represents the decision tree algorithm, where the nodes are created from the most relevant control variables for each segment of the tree. This allows the final metric tree6 to evaluate many variables and still have fewer buckets or terminal nodes. Additionally, the trees can be limited so that the splitting ends if the number of loans falls below a certain threshold, ensuring that each terminal node contains a sufficient number of observations to make valid comparisons. Note that the example tree does not represent any particular metric in the STAR Scorecard; rather, it is a simple representation of the way the tree branches and nodes are created based on the attributes provided to the partitioning algorithm. To simplify the example, the outer branches of the sample tree have been limited so that just the first four levels are visible, and continuous variables like LTV have been rounded. Not all nodes are labeled in the image below but since the splits are binary, the alternate node represents the opposite of the inequality represented.

Figure 2: Comparable Pool "Tree" Methodology

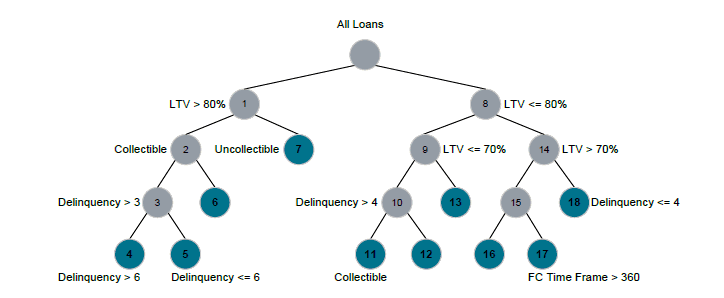
In this example the algorithm has determined that the most important segmentation for the entire metric is LTV and has first split the population based on those loans with an LTV greater than 80% or less than or equal to 80%. For loans with higher LTVs, the next segmentation is whether or not there are circumstances that would limit a servicer’s ability to collect a payment (e.g., bankruptcy, forbearance, etc.). The collectible population is then further split by delinquency, while for loans that are deemed uncollectible the node terminates and there is no further segmentation for that population of loans.

For loans with lower LTV ratios, the next node level further defines the population in terms of the same LTV. This is a valuable feature of the recursive partitioning methodology that allows attributes to be refined as they progress through the tree. The final splits are based on the delinquency of the loans and then the collectability or foreclosure time frame. As mentioned previously, it is the performance at the final, terminal node level that is used to create the Comp for each credit performance metric.

In the following section, we will select two terminal nodes from this tree that represent loans that might be considered more or less likely to achieve a curative event in the sample metric. We will then compare two servicers’ performance in those nodes to demonstrate how servicers’ portfolio characteristics impacts the construction of their Comp, and how servicer performance is evaluated relative to the Comp performance.

Summary

The attributes used to establish comparable portfolio characteristics for each metric are chosen based on analysis performed by Fannie Mae. The STAR Scorecard methodology uses decision trees to segment portfolios based on specific loan attributes. The attributes are chosen based on historical analysis performed by Fannie Mae, and the variables are then selected by a partitioning algorithm that segments the populations based on the how the attribute differentiates performance.

 

4 Torsten Hothorn, Kurt Hornik, Achim Zeileis (2006). party: A Laboratory for Recursive Partytioning.

5 Splits can be either groupings of categorical variables like collectability or thresholds for continuous variables like LTV.

6 Trees for each metric are developed and calibrated using the entire Fannie Mae portfolio. The final tree for each metric is then applied to each servicer’s population of loans.